Scaling of Star Polymers
Daoud-Cotton Blob Model

A star polymer can be described as a cluster of linear chain molecules joined together at the center. The monomer concentration will vary with the distance from the center. In the case of a many-arm star polymer, the concentration in the core of the star is very high while the monomer concentration in the outer region is very low because the branches are relatively far apart from each other and therefore behave in a similar way as a single (linear) chain molecule. In the case of spherical symmetry, the mean monomer concentration will be only a function of the distance from the center. This is also true for a single linear chain molecule, if we define the central point as the center of gravity.¹ But in contrast to a linear polymer the assumption of a constant swelling parameter is incorrect. Instead, the swelling will vary with the distance to the center.

Scaling in a Section of a Star-branched Polymer

The variation of the local concentration can be described with the blob theory of Pierre-Gilles de Gennes.² This theory was first applied to star polymers by M. Daoud and J.P. Cotton.³ In their model, every branch consists of a succession of subunits, the so called blobs, with a size ξ(r) increasing from the center of the star to the outside. The size of each blob can be estimated from the self-similarity around the central point; all blobs of same size have the same distance to the center of the star. Then the number of blobs in each blob layer is equal to the number of branches. Furthermore, the blobs in each layer completely cover the sphere so that the size of a blob is directly proportional to the distance from the center of the star. From these assumptions it follows that the local segment concentration φ(r) is identical with the segment concentration in the f blobs of size ξ(r) enclosing g repeat units of length l:

φ(r) ≅ φ_blob ≅ l³g / ξ³(r)

To calculate φ(r), the local swelling parameter α has to be known,

ξ(r) = α ξ₀(r).

where ξ₀(r) is the unperturbed size of a blob. Inside the blob, the sub-chain behaves like a single chain, so that Flory's excluded volume theory applies to the subchain as well,

α⁵ - α³ ≅ (1 - 2χ) g^1/2 ≅ νg^1/2 / l³

where χ is the Flory-Huggins interaction parameter and ν is the effective excluded volume. If g >> 1, the second term on the left-hand side can be neglected, it follows

α⁵ ≅ νg^1/2 / l³

With this relation, the segment volume fraction can be rewritten as

φ ≅ l³g / (αξ₀)³ ≅ α^-3 g^-1/2 ≅ ν^-3/5 g^-4/5

and

ξ ≅ α ξ₀ ≅ g^3/5ν^1/5l ;    α(r)² ≅ νgφ(r)

If we assume that all blobs of the same size ξ(r) have the same distance to the center of the star, then each shell between two spheres of radius r and r+ξ contains the same number of blobs, which is equal to the number of branches f, thus the volume fraction scales as

φ ≅ g f l³ / (r²ξ)

The mean monomer concentration is also a function of the number of branches f, since f blobs completely cover the sphere of radius r so that

r² ≅ f ξ²   or   ξ ≅ r / f^1/2

Combining these equations, one easily verifies that the monomer concentration scales as

φ ≅ g f^1/2 l³ / r³ ≅ f^2/3 / (ν^1/3r^4/3)

With g = φ(r)ξ³ the number of monomers inside a blob can be written as

g ≅ r^5/3 / (f^5/6ν^1/3)

The equations above describe only the outer region of the star. In the inner region, the blobs are closely packed and are therefore unswollen. The crossover distance r_cr can be calculated from the condition α(r_cr) = 1:

r_cr = f^1/2ν^-1l

In the inner region r < r_cr, the subchains of the blobs behave like ideal chains, so that

ξ ≅ g^1/2l   and   φ ≅ g^-1/2.

The scaling relations for the physical quantities in the center region can be derived in an analogous manner:³

g(r) ≅ (r/l)² / f
ξ(r) ≅ r / f^1/2
φ(r) ≅ f^1/2 / (r/l).

The very core of the star polymer consists of closely packed monomers, so that φ, ν ≈ 1. It follows that

r_core ≅ f^1/2l

Then ξ and g are also of order unity, meaning a blob is just one repeat unit.

The concentration profile of the three regions is shown schematically in the figure below. Note, for an athermal solvent (ν = l³), the intermediate region disapears (r_core = r_cr) .

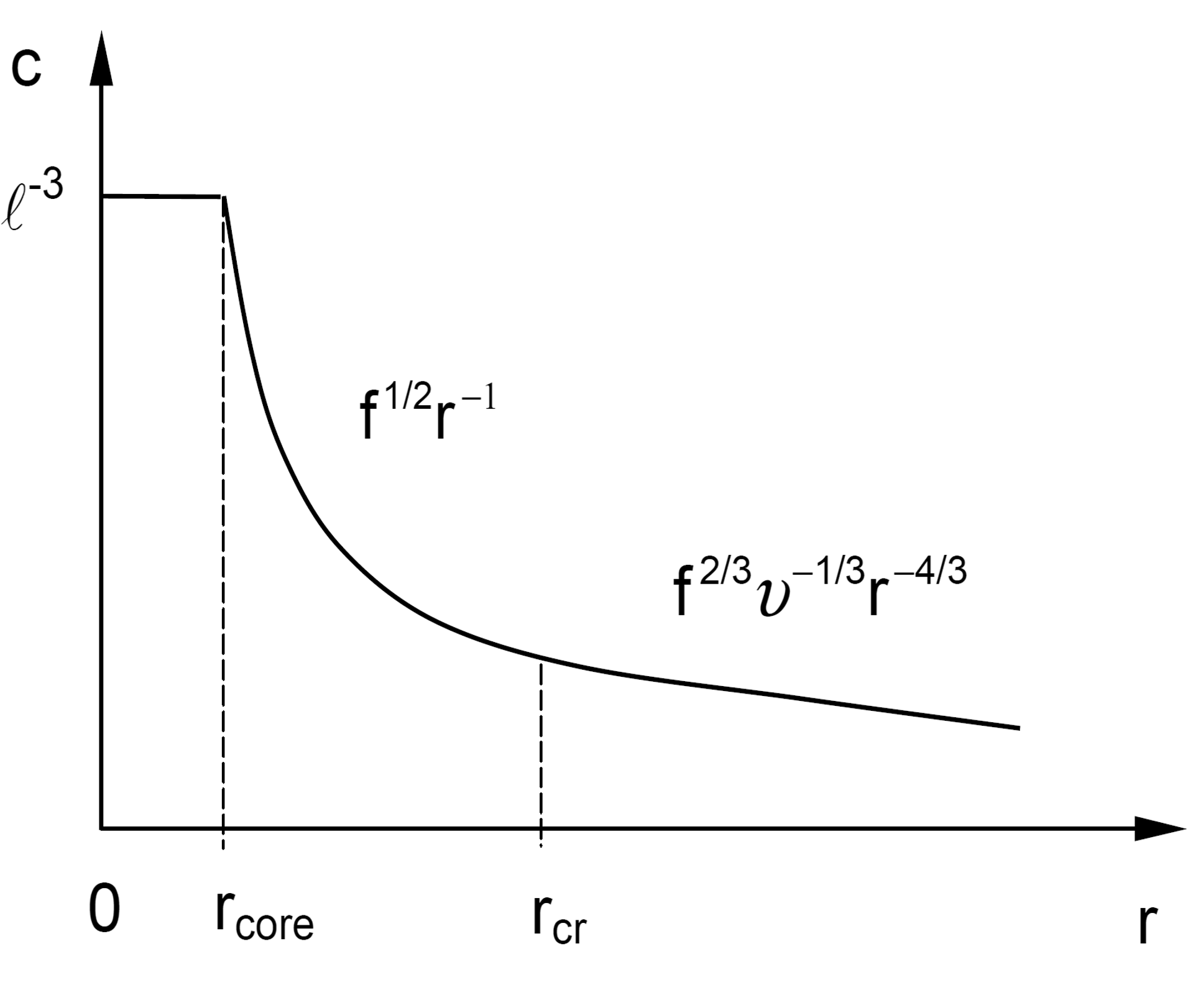
Concentration Profile Inside a Star Polymer

References & Further Readings

1. P. J. Flory, J. Chem. Phys. 9, 660 (1941); 10, 51 (1942); 17, 303 (1949)
2. P.G. de Gennes, Scaling Concepts in Polymer Physics, Cornell University Press (1970)

3. M. Daoud, J.P. Cotton, J. Phys. (Paris) 43, 531 (1982)

4. E.A. DiMarzio, C.M. Guttman, J. Phys. Chme. 93, 7004 (1989)
5. A. Halperin, Macromolecules 20, 2943 (1987)
6. A. Halperin and S. Alexander, Macromolecules, 20, 1146 - 1152 (1987)
7. E.A. Di Marzio, C.M. Guttman, A. Mah, Macromolecules 28, 2930 (1995)
8. I. Teraoka, Polymer Solutions: An Introduction to Physical Properties, John Wiley (2002)
9. A. Y. Grosberg, A.R. Khokhlov, Statistical Physics of Macromolecules, AIP Press (1994)
10. M. Rubinstein and R. Colby, Polymer Physics, 1st Ed., Oxford University Press (2003)